SVM-支持向量机
0x00
有些书上写:“SVM是最好的现成分类器”,意思就是不用调参什么的,直接拿一个通用的SVM分类器去训练,模型就会表现得很不错。
0x01 基本原理
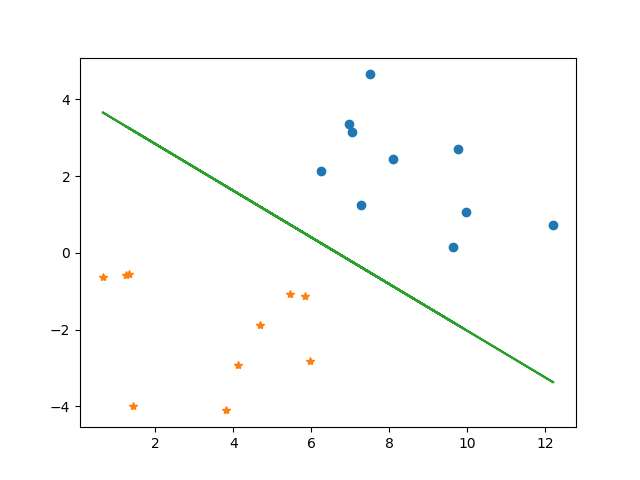
假如有两类数据集,如下图所示,希望能找到一条直线,能把这两类数据给划分开,并且使得每个样本到直线的距离最大。
直线方程可以用以下公式表示,其中$\omega$是法向量,$x$为样本空间,: $$ \omega^Tx + b = 0 $$
这个直线也被叫做为超平面(在高维中,如果样本时n维的,那么超平面是n-1维),那么样本空间种任意点x到超平面的距离为:
$$ \gamma = \frac{\omega^Tx + b}{||\omega||} $$
如果要使得最大化间隔,(这里省略了若干推导),最终我们得到的目标函数为:
$$
\min_{w,b} \frac{1}{2} || \omega ||^2 \\
s.t. \ y_i(\omega^Tx_i+b) \geqslant 1 ,\quad i =1,2,…,m.
$$
对于有约束条件的求极值问题,一般可以选择用拉格朗日乘子法来进行求值,基于上面的目标函数 $f(\omega)$ ,然后我们让加上 $\alpha$ 倍的约束函数 : $L(\omega, b, \alpha) = f(\omega) + \alpha\phi(x)$, 按照这种形式,我们的目标函数可以写成:
$$ L(\omega, b, \alpha) = \frac{1}{2} || \omega ||^2 + \sum_{i=1}^{m}{\alpha_i (1 - y_i(\omega^Tx_i+b))} $$
其中 $\alpha = (\alpha_1;\alpha_2;…;\alpha_m)$. 令
$$
\frac{\partial{L(\omega, b, \alpha)}}{\partial{\omega}} = 0 \\
\frac{\partial{L(\omega, b, \alpha)}}{\partial{b}} = 0$$
可得,
$$\omega = \sum_{i=1}^{m}{\alpha_i {y_i} {x_i}} $$
$$\sum_{i=1}^{m}{\alpha_i {y_i}}= 0$$
把上面两个结果代入到上一个目标函数,得到最终的目标函数:
$$ \max_{\alpha} \ \sum_{i=1}^m \alpha_i - \frac{1}{2} \ \sum_{i=1}^{m}\sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j x_i^T x_j$$
这样我们消元掉$\omega$ 和 b 后,剩下就是求出 $\alpha$ 的值, 然后再通过 $\alpha$ 求出 $\omega$ 和 b。求解上面的目标函数 ,有个著名的算法叫SMO,实际上这个就是一个二次规划问题。
0x02 简单的二分类
更多的细节暂时不展开,现在我们大概明白SVM的大概原理了。 回到一开始的问题,我们需要找出一个超平面来划分我们的样本空间,下面用sklearn简单实现了下:
from sklearn.svm import SVC
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
def draw_boundary2D(coef_, intercept_, X1, ax=None):
"""
画出我们的超平面
"""
for index, intercept in enumerate(intercept_):
weights = np.insert(coef_[index], 0, intercept)
X2 = (-weights[0] - weights[1] * X1) / weights[2]
if not ax:
ax = plt.subplot()
ax.plot(X1, X2)
def separate_data(X, labels) -> list:
"""
把原始数据按照label分开,方便画图
"""
datas = dict(((label, []) for label in set(labels)))
for x, label in zip(X, labels):
print(type(x))
datas[label].append(x)
return list(datas.values())
def draw(X, y, coef_, intercept_):
"""
画图
:param X: 样本数据
:param y: 样本对应的标签
:param coef_: 超平面参数W
:param intercept_: 超平面参数b
:return:
"""
datas = np.array(separate_data(X, y))
ax = plt.subplot()
for i in range(len(datas)):
ax.plot(np.array(datas[i])[:, 0], np.array(datas[i])[:, 1], 'o')
X1 = X[:, 0]
draw_boundary2D(coef_, intercept_, X1, ax=ax)
plt.show()
if __name__ == '__main__':
X, y = datasets.make_blobs(n_features=2, centers=2, n_samples=20, cluster_std=2.0) # 生成样本
clf = SVC(kernel='linear') # 使用线性核函数,默认是rbf
clf.fit(X, y) # 训练数据
draw(X, y, clf.coef_, clf.intercept_)
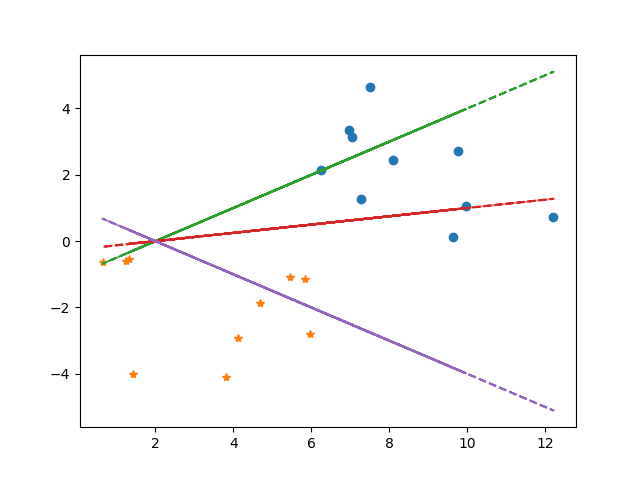
程序看起来很多,但是实际上我们利用sklearn来训练我们的样本得到我们的模型也就至用了两行。
0x03 多分类问题
从最上面介绍的基本原理可以看出,SVM一开始设计是用来解决二分类问题的。但是SVM也可以用来解决多分类的问题,一般有两种方法:
- 通过对最原始的最优化问题进行修改,将多个超平面的参数合并到一个最优化问题里。但是这个求解过程太过复杂,计算量大,而且实现困难,所以一般现实问题都不会这样做。
- 另外一种就是把多分类问题拆分成若干个二分类问题进行求解,最后合并最优结果。这类求解方法又分为两种:
OVR和OVO.- OVR:全拼One-Vs-Rest, 这种方法也被叫做一对多。这种方法会将每一类样本用一个分类器去进行拟合。对于每一个分类器,该类会将其他所有类进行区分。这种方法优点在于计算量少,可解析。缺点就是当分类比较多的时候,会出现1:m这样的biased问题。
- OVO:全拼One-Vs-One,这种方法又叫一对一。这种方法会将每两类之间做一个分类器,这样就会产生 $\frac{n(n-1)}{2}$个分类器。好处在于这样可以避免掉样本不均衡的问题,但是同样大量增加了的训练和预测的计算量。不过一般生产环境为了效果更佳,会选择OVO。
- 所以对于类别不多但是样本量很多的情况下,OVR表现会更好;但是对于样本种类多,准确率有很高要求的,选择OVO会更好。
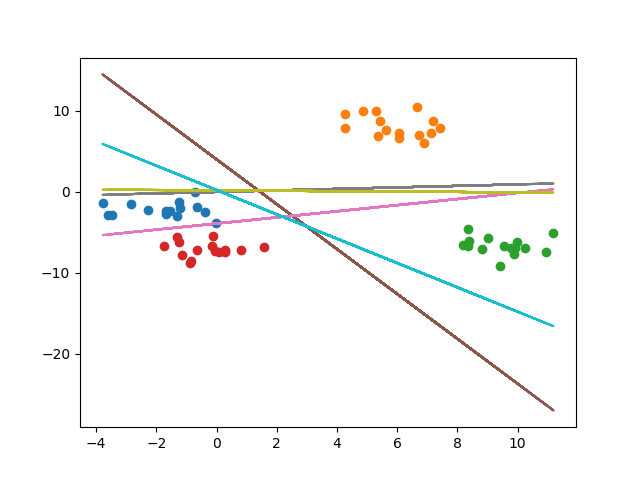
Sklearn同时提供了OVR和OVO的封装, 下面做两个简单的例子:
OVR
from sklearn.multiclass import OneVsRestClassifier
from sklearn.svm import LinearSVC
class_count = 4
X, y = datasets.make_blobs(n_features=2, centers=class_count, n_samples=class_count * 15)
clf = OneVsRestClassifier(LinearSVC())
clf.fit(X, y)
coef = [estimator.coef_[0] for estimator in clf.estimators_]
intercept = [estimator.intercept_[0] for estimator in clf.estimators_]
draw(X, y, clf.coef_, clf.intercept_)
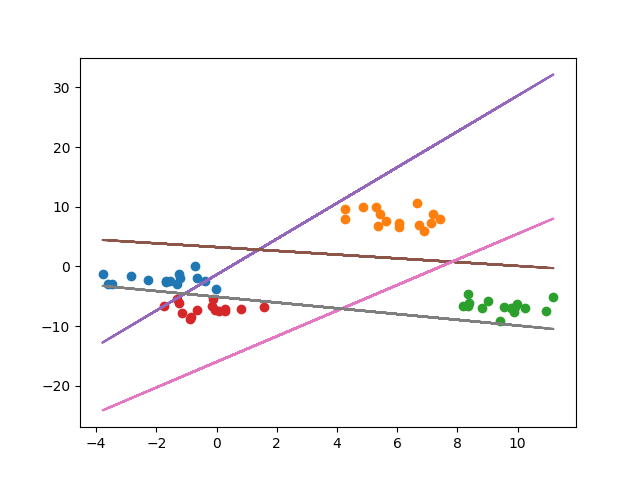
OVO
from sklearn.multiclass import OneVsOneClassifier
clf = OneVsOneClassifier(LinearSVC())
clf.fit(X, y)
coef = [estimator.coef_[0] for estimator in clf.estimators_]
intercept = [estimator.intercept_[0] for estimator in clf.estimators_]
draw(X, y, coef, intercept)
0x04 核函数
前面提到的分类问题,前提都是样本是线性可分的,那么对于样本是线性不可分的情况下,让样本X投影到更高维空间中 $x\mapsto \phi(x)$,使得样本在这个特征空间下,可以合适的划分超平面。
比如像下面的这两类数据,在二维空间中找不到一个直线能将这两类数据区分开,不过我们通过观察,发现可以用一个类似椭圆的曲线将这两类区分开。
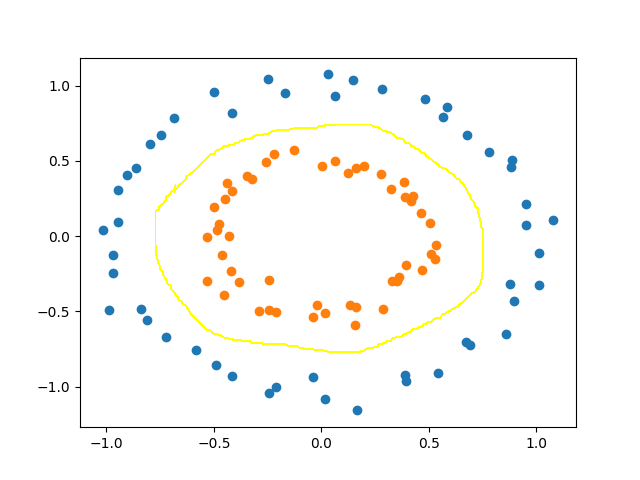
我们可以尝试通过以下映射,映射到维数更高的三维空间中:
$$
\left(
\begin{aligned}
x1 \\
x2
\end{aligned}
\right) \Rightarrow
\left(
\begin{array}
x1 \\
x2 \\
x1^2 + x2^2
\end{array}
\right)
$$
显然,在三维空间中,存在一个超平面可以区分开这两类数据
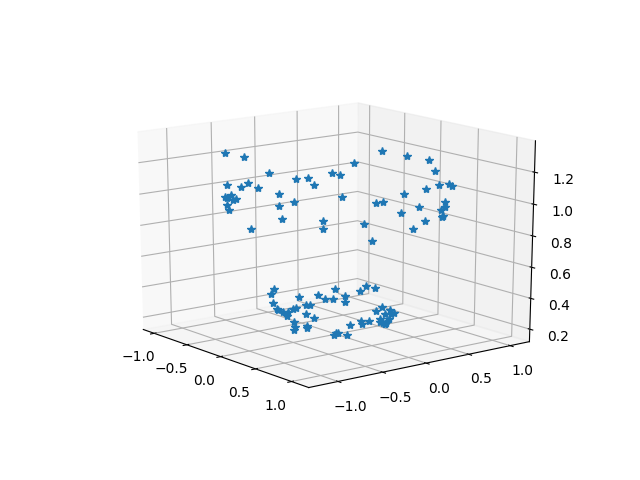
我们的原函数 $f(x) = \sum_{i=1}^N{w_ix_i + b}$ 经过映射之后的表示为:
$$ f(x) = \sum_{i=1}^N{w_i\phi(x_i) + b} $$
常用的核函数有:
| 线性核 | $$ k(x, y) = x^Ty + c $$ |
| 多项核 | $$ k(x, y) = (ax^Ty + c)^d $$ |
| 径向基核(RBF)又称高斯核 | $$ k(x, y) = exp(-\gamma|| x-y || ^2) or \\\ k(x, y) = exp(-\frac{ || x-y || ^2}{2\delta^2}) $$ |
| 幂指函数核 | $$ k(x, y) = exp(-\frac{|| x-y || }{2\delta^2}) $$ |
| 拉普拉斯核 | $$ k(x, y) = exp(-\frac{|| x-y || }{\delta}) $$ |
| Sigmoid核 | $$ k(x, y) = tanh(ax^T+c) $$ |
我们这里重点说一下高斯核,也就是径向基核函数,简称RBF。在Sklearn里面Svm模块默认的kernel就是rbf。径向基核函数,顾名思义,取值仅仅依赖特定点距离的实值函数,也就是 $\phi(x, y) = \phi(||x-y||)$ 。只要满足$\phi(x, y) = \phi(||x-y||)$都叫径向量函数,一般我们都是用欧式距离。
在用SVM模块时候进行分类的时候,Sklearn提供了很方便的接口让我们去调用,下面举个调用不同kernel的例子:
from matplotlib import pyplot as plt
import numpy as np
from sklearn.svm import SVC
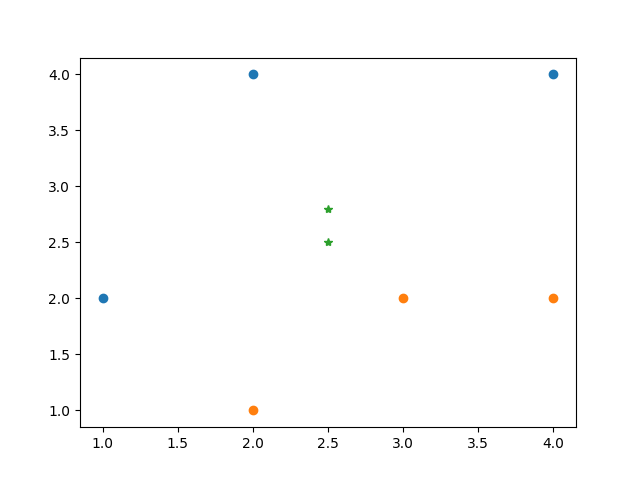
X = [[1, 2], [2, 4], [4, 4], [2, 1], [3, 2], [4, 2]]
y = [0, 0, 0, 1, 1, 1]
evaluate_data = np.array([[2.5, 2.5], [2.5, 2.8]])
kernels = ['linear', 'poly', 'rbf', 'sigmoid']
datas = np.array(separate_data(X, y))
ax = plt.subplot(111)
for i in range(len(datas)):
ax.plot(np.array(datas[i])[:, 0], np.array(datas[i])[:, 1], 'o')
ax.plot(evaluate_data[:, 0], evaluate_data[:, 1], '*')
for index, kernel in enumerate(kernels):
clf = SVC(kernel=kernel, probability=True) # 使用线性核函数,默认是rbf
clf.fit(X, y) # 训练数据
print(clf.predict_proba(evaluate_data)) # 用这个模型预测 (2.5, 2.5), (2.5, 2.8)这两个点的分类结果概率
plt.show()
最终结果输出如下:
>>>[[0.56740906 0.43259094]
[0.61265554 0.38734446]]
>>>[[0.53774676 0.46225324]
[0.58272179 0.41727821]]
>>>[[0.3932861 0.6067139]
[0.1732895 0.8267105]]
>>>[[0.5 0.5]
[0.5 0.5]]
从结果我们可以看出,不同kernel预测的结果都不一样,所以不同kernel拟合出来的超函数也是不一样的。所以在我们选择kernel的时候,需要观察数据的特点,不然即使我们使用kernel函数把原函数映射到高维空间后,还是找不到一个可以对样本进行划分合适的超平面。